Арбузный блог

Миф о листе бумаги, который якобы нельзя сложить вдвое больше семи-восьми раз, снова потерпел сокрушительное поражение. На сей раз не устоял рекорд, державшийся целое десятилетие, – американские студенты побили его с помощью туалетной бумаги.

(далее…)

Автор: Юрий Ильин Опубликовано 26.03.2012 в блоге автора (rss)

Довольно странный «рисовальный аппарат» соорудил студент-дизайнер Роберт Хоузар. Он взял два старых проигрывателя, закрепил на них конструкцию из четырёх реек, на конце которой бельевая прищепка держит гелевую ручку (так что получилось что-то вроде пантографа), и заставил диски вращаться с разной скоростью.

Рисунки, сделанные конструкцией Роберта Хаузара (ссылка с изображения ведёт на сайт автора)

В результате такой «рисующий аппарат» производит на свет «математически выверенные» изображения, которые, возможно, и не отличаются особой художественной ценностью, но всё-таки несколько завораживают.

(далее…)

Поселились на системном блоке: приехали из Израиля от Лилии Яковлевны. Спасибо! Прикольные.

Четырнадцатое число третьего месяца отмечается во всем мире ка День Пи потому что 3.14!

В этот день рекомендуется рассматривать округлые предметы и рассуждать об отношении длины окружности к ее диаметру.

я проделываю одну и ту же процедуру: подправляю футер (подвал), меняю дату при антикопирайте, сейчас это выглядит так:

)c( 2000-2012  Kопирайта нет, копируйте на здоровье :)

 

1100₂ года в Интернете

Сегодня Арбузу исполнилось 12 лет!

Он родился 29 февраля 2000 года (тогда еще столько споров было, високосный ли 2000-й год и почему, не помните?). Дни рождения в високосные годы особенно трогательны, это уже третье!

История рождения и взросления можно прочесть в статье «Почему Арбуз?»

Спасибо всем, кто помогал и помогает с математическими чудесами, задачками, геометрическими и арбузными картинками! Сам бы я все это не собрал бы… Спасибо читателям, решателям и всем, кто знает про Арбуз и арбузный блог!

Сергей и Марина Бондаренко

Возможно, одна из фантазий Артура Кларка скоро станет явью, как когда-то стала реальностью подводная лодка Жюля Верна. Японская компания Obayashi Corp. заявила о том, что намерена реализовать невероятно амбициозный проект — построить космический лифт.

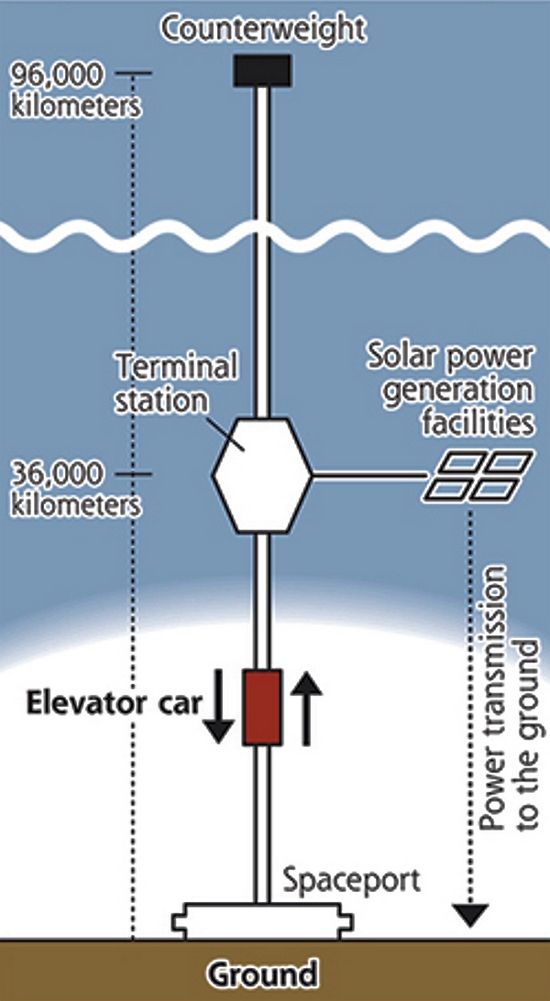
Да-да, именно лифт, который будет поднимать грузы и, возможно, людей с Земли на околоземную орбиту. Конструкция такого невероятного сооружения будет основана на специальном тросе, сделанном из тонких и сверхпрочных углеродных нанотрубок. Этот трос будет иметь длину 96 тысяч километров.

(далее…)

Чёрт побери, заканчивается 21.02.2012 — когда еще будет такая симметричная дата?