С Хабра.

Я обнаружил этот фрактал, когда разглядывал интерференцию волн на поверхности речки. Волна движется к берегу, отражается и накладывается сама на себя. Есть ли порядок в тех узорах, которые создаются волнами? Попробуем найти его. Рассмотрим не всю волну, а только вектор ее движения. «Берега» сделаем гладкими, для простоты эксперимента.
Эксперимент можно провести на обычном листке в клеточку из школьной тетради.
(далее…)
Не так давно попалась мне на глаза великолепная юмористическая статья про файловую систему, хранящую данные в числе Пи. Бурное обсуждение, развернувшееся в комментариях (кажется, не все его участники поняли шутку), натолкнуло меня на мысль, что тему нормальных чисел неплохо бы обсудить более серьёзно, тем более что тема эта благодатна, полна красивых результатов, нерешённых проблем и прочих кошерных вещей. Если желаете с этими вещами ознакомиться — пожалуйте под кат.

(далее…)
Вторник, 3 Сентябрь, 2013 | Рубрика:
Всячина
Теорема Пифагора: физическое доказательство.

Ну ведь прелесть же! И притом преизящная :)
.
Источник.
Вторник, 25 Июнь, 2013 | Рубрика:
Всячина
Источник Хабрахабр.

Карл Гаусс, в своё время, назвал математику царицей всех наук, отдавая ей особое место в сфере человеческого знания. Действительно, совершенно непохожая на другие науки, она скорее служит для них языком или методом изучения. Являясь, пожалуй, самой строгой из всех наук, она не имеет собственного строгого и общепринятого определения. На протяжении всей своей истории, преобразуясь сама, преобразовывалось и понятие о математике. Учёные, в течении всего развития математики, смогли составить скорее не определения математики, а набор афоризмов характеризующий её или представления о ней.
«Математика — это язык, на котором написана книга природы»(Г. Галилей)
«Математика – это наука о необходимых заключениях»(Б. Пирс)
«Математика – это строгий язык, служащий для перехода от одних опытных суждений, к другим»(Н. Бор)
«Математика – это иерархия формальных структур»(Н. Бурбаки)
«Математика — это наука о количественных отношениях и пространственных формах действительного мира»(А. Колмогоров)
— это лишь малая часть суждений, показывающая разнородность представлений о математике. Помимо вопроса определения математики, интересными и дискуссионными являются вопросы о её природе(основаниях), её методологии, целях и связи с реальным миром. Ответы на них также неоднозначны и значительно изменялись со временем, создавая различные философские течения.
31 августа 2012 года японский математик Cинъити Мотидзуки опубликовал в интернете четыре статьи.
Заголовки были непостижимы. Объём был пугающим: 512 страниц в сумме. Посыл был дерзким: он заявил, что доказал abc-гипотезу, знаменитую, соблазнительно лёгкую числовую теорию, которая десятилетиями заводила математиков в тупик.
Затем Мотидзуки просто ушёл. Он не отправил свою работу в Annals of Mathematics. Он не оставил сообщение ни на одном сетевом форуме, которые часто посещают математики со всего мира. Он просто опубликовал статьи и ждал.
Два дня спустя, Джордан Элленберг, профессор математики в Висконсинского университета в Мадисоне, получил почтовое оповещение от Google Scholar, сервиса, который сканирует интернет в поисках статей по указанным темам. Второго сентября Google Scholar отправил ему статьи Мотидзуки: «Это может заинтересовать вас».
«А я такой: „Да, Гугл, мне это как бы интересно!“» – вспоминает Элленберг, – «Я запостил их в Фэйсбуке и в моём блоге, с пометкой: „Между прочим, похоже, что Мотидзуки доказал abc-гипотезу“».
Интернет взорвался. В течение дней даже далёкие от математики СМИ подхватили историю. «Решена сложнейшая в мире математическая теория», – объявила Telegraph. «Возможный прорыв в abc-гипотезе», – немного скромнее писала New York Times.
(далее…)
Понедельник, 1 Апрель, 2013 | Рубрика:
Иллюзии
Здесь. можно посмотреть и код странички.
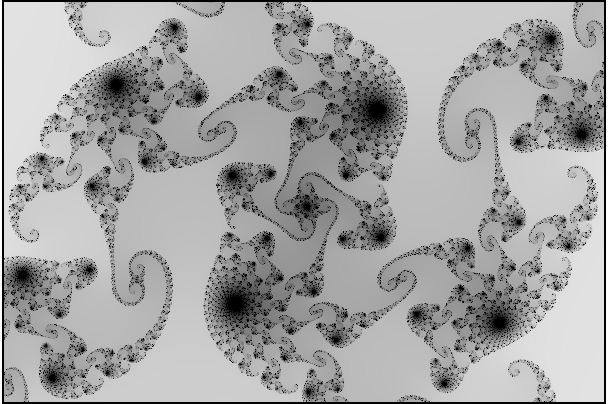
Четверг, 10 Январь, 2013 | Рубрика:
Чудеса
Эту игрушку купил сотрудник около Цирка, забавная штука, легко меняет форму, и красивая. Стоит 6000, но отдает хозяин и за 5000 если поторговаться.

(далее…)
Вторник, 18 Декабрь, 2012 | Рубрика:
Новости
Совместный проект ZiyoNET и X-Places.uz
Приглашаю всех на лекцию по занимательной математике «До и после компьютера». Состоится 22 декабря в Национальной библиотеке им. Навои в 13:00.

Никаких сложных задач — увлекательное путешествие по чудесам.
Желающие пойти — регистрируемся на Письмах о Ташкенте, на юФоруме или в группе X-Places в Фейсбуке.
Вход по паспортам, надо указать полные ФИО. Регистрация в среду и до вечера четверга 20 декабря, так как в пятницу утром сформированные списки вместе со списком от X-Places соорганизатор Рустам Хусанов передаст в библиотеку.
Приходите, будет интересно, вряд ли вы еще такое услышите :-0)

КАМЕННАЯ РЕЗНАЯ РЕШЕТКА. ИНДИЯ. XVI ВЕК.
Уникальный тип орнамента на основе восьмиконечных звезд со свастикой в центре. Изготовлена в период правления внука Бабура Акбар-шаха (1556-1605). Материал — красный песчаник. Музей Метрополитен, Нью-Йорке, Роджерс фонд, 1993.




 Карл Гаусс, в своё время, назвал математику царицей всех наук, отдавая ей особое место в сфере человеческого знания. Действительно, совершенно непохожая на другие науки, она скорее служит для них языком или методом изучения. Являясь, пожалуй, самой строгой из всех наук, она не имеет собственного строгого и общепринятого определения. На протяжении всей своей истории, преобразуясь сама, преобразовывалось и понятие о математике. Учёные, в течении всего развития математики, смогли составить скорее не определения математики, а набор афоризмов характеризующий её или представления о ней.
Карл Гаусс, в своё время, назвал математику царицей всех наук, отдавая ей особое место в сфере человеческого знания. Действительно, совершенно непохожая на другие науки, она скорее служит для них языком или методом изучения. Являясь, пожалуй, самой строгой из всех наук, она не имеет собственного строгого и общепринятого определения. На протяжении всей своей истории, преобразуясь сама, преобразовывалось и понятие о математике. Учёные, в течении всего развития математики, смогли составить скорее не определения математики, а набор афоризмов характеризующий её или представления о ней.
























