Арбузный блог

Так называется это фото — как-будто всего-лишь геометрия…

Это отголоски жюрения Премии Казнета — источник

Нитка і кільце. На вертикально встановленій дошці у точках A i B закріплені кінці нитки довжиною l>AB Відрізок AB утворює гострий кут  a з ве-ртикальним напрямком. У стані рівноваги кільце з важком зайняло положення у точці C Знайти відношення, у якому кільце ділить нитку. Масою нитки знехтувати.

Это задачу запостили в Арбузный форум. Ответ можно выложить на узбекском ;-)

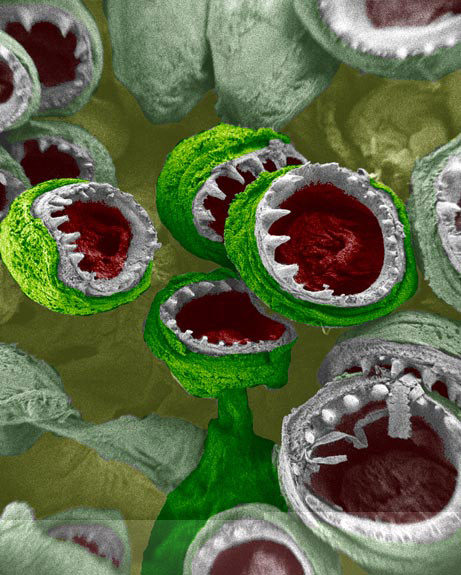
Эти «зубастые монстры» на самом деле – крошечные присоски на щупальцах ребристых кальмаров Loligo pealei (фото Jessica D. Schiffman, Caroline L. Schauer; Drexel University/Science). Источник — Мембрана.ру

Две статьи на Хабре, рекомендую, интересно — первая и вторая.

Настоятельно рекомендую всем любителям занимательной математики посетить http://www.archimy.com/.

Выбираете модель — и получаете ее на экране в трехмерном виде, можно, вращая мышкой, обозреть со всех сторон. Меняя параметры в уравнении и отслеживая эти изменения на получившейся поверхности забудете обо всем на свете :-)

Сера в комбинации с другими минералами окрашивает кратер вулкана Даллол, находящегося в Эфиопии, в зеленоватые оттенки. Даллол находится на отметке 48 метров ниже уровня моря и является самым низким расположенным на суше вулканом.

Обратите внимание на то, как природа замостила плоскость — сколькиугольники для этого использованы? ;-)

На «Планете школ» есть флешевые игры, и среди них — «Крестики-нолики». Если первым ходит человек (то есть, вы), то он, естественно, ставит крестик в центральную клетку. Программа должна ответным ходом поставить нолик в угловую клетку — иначе проигрыш. Но она не ставит в угловую, ставит в серединную одной из граней. Не всегда, правда, иногда ставит в угол, но редко. Я спросил разработчика — почему не всегда в угол — заведомо проигрыш же? Он говорит — должны же школьники хоть иногда выигрывать ;-) Можете попробовать — глупо, но приятно выиграть у программы! :-)

На этом сайте, стоит посмотреть его картины, например, такие:

Отсюда

Рассмотрите внимательно первый рисунок — можно ли его нарисовать не отрывая руки от бумаги? И второй — кроме пяти маленьких вставок — это одна линия или несколько? Сможете ли повторить? А по памяти? :-)

Так называется целый фильм, обучающий живописи на примере одного натюрморта… естественно с арбузом ;-)

Подсказал адресок ne0d1n

Группы математиков из США и Германии обнаружили два самых больших простых числа в истории. Данное открытие может значительно увеличить эффективность систем шифрования, применяемых в современной вычислительной технике. Оба числа были открыты с разницей в пару недель и каждое в рамках проекта Great Internet Mersenne Prime Search (GIMPS), длящегося уже 12 лет.

Самое большое простое число было обнаружено 23 августа учеными из Университета Калифорнии, это число содержит 12 979 189 цифр. Второе число, содержащее 11 185 272 цифры, было обнаружено двумя неделями раньше в Германии.

Напомним, что простые числа — это такие числа, которые делятся без остатка только на самих себя и на единицу. В основе математических особенностей таких чисел лежит принцип действия многих систем криптографии.

Спонсирует поиск крупнейших простых числе фонд EFF (Electronic Frontier Foundation), который намерен в перспективе создать систему шифрования данных, которую без ключа взломать невозможно в принципе.

Источник

Источник

Что именно?

Еще пять картинок-иллюзий под катом

(далее…)