Владимир, который Z__Z выложил в Арбузном форуме чью-то рожу. Обратите внимание на технику исполнения — чем темнее участок, тем чаще в нем точки равного радиуса. Владимир предложил забить гвоздь в каждую точку — получится псевдо 3D-рожа.
Nigma.ru добавила в свою копилку новую фичу для пользователей. Теперь прямо через строку поиска можно решать различные математические задачи, например, x2-3x+2=0, sin2 x + cos2 x, 2 ч * 30 м/мин = х, системы уравнений типа 2x-y=4, 3y+x=9, x2+y=1, x*y=0 и т. п. (подробный список тут). Сервис рассчитан на школьников 6-10 класса.
Подробнее о системе можно узнать, прочитав документацию и новость на нашем сайте.
Такое противоречие — создал динамит (самое большое зло для войны) и учредил премии — важный стимул развития человечества. Статья про него «Динамит как лучшее средство против войны«
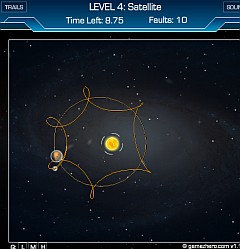Orbitrunner — непростая игрушечка. Сюжет простой — «ты звезда». Мимо тебя летит планета, иногда со спутником (луной) иногда даже с двумя. Задача — не дать упасть планете на звезду или улететь за пределы орбиты. Детишкам хорошо показывать примеры взаимодействия небесных тел между собой. Дальше 14 уровня уже очень сложно начинается.
Я вот что думаю… Есть ли в этой игре учет немоментального распространения гравитации? Было бы так же неплохо сделать передвижение солнца хоть как-то близким к физическим принципам. А то диаметр солнца (звезды) может доходить до нескольких световых минут и я его двигаю как бы и быстрее скорости света… Тоже непорядок.
При этом я тут подумал об очень интересном эффекте: если быстренько переместить (телепортировать) звезду в иное место, допустим, за орбиту планеты, но поближе, чем она была, раза в два — то некоторое время планета по гравитации и по излучению будет существовать в системе 2 солнц, хотя в реальности солнце будет одно. Фантастика конечно, но теоретически я не вижу препятствий.
Источник — Кулер
Правила просты — за минимальное количество ходов переставить красные шары в красные круги, зеленые шары — в зеленые круги.
В идеале это 40 ходов — меньше врядли получится :)
Шары перемещаются как и конь на шахматной доске — буквой Г.
При клике на шар он переместится в свободную клетку, если такая имеется только одна для данного шара. Если шар можно переместить в две и более клеток — варианты куда можно поставить шар будут мигать и надо будет нажать на соответствующей клетке, либо по другому шару.
Имеется в наличии: картина, веревка, два гвоздя, вбитых в стену.
Нужно: повесить картину на стенку так, чтобы при вытаскивании любого из гвоздей она падала.
но мы живем на внутренней поверхности шара, если вы еще не в курсе этой теории, то можете познакомиться с ней.
Вследствие утраты углом остроты, заключенная здесь сила становится
хотя и менее агрессивной, но более длительной Угол заключает в себе
нечто бездумно юношеское, кривизна — зрелую, по праву уверенную в себе энергию.
Василий Кандинский. Точка и линия на плоскости
Есть чем заняться скучными осенними вечерами, когда по летней инерции еще хочется погулять подольше, а зимняя спячка еще не окутала молодящийся разум. И так, берёте лист бумаги и рисуете замысловатую с самопересечениями замкнутую линию. Представим, что это дорога, точнее автострада. Будем по ней двигаться из произвольно выбранной точки. Каждое пересечение (предположим, что в точках пересечения пересекаются не более двух линий) будем рассматривать как перекресток, и не простой, а с развязкой в двух уровнях. Будем также следовать правилу — чередовать уровни — если первый перекресток мы проезжаем «сверху», то следующий «снизу» относительно пересекаемой дороги. Наша автострада будет то над, то под пересекаемых участков. Рисование таких трасс хорошее занятие на скучных заседаниях, на уроках, лекциях и семинарах.
Это было вступление, так сказать раздаточный материал, с которым мы сейчас будем работать. Собственно говоря, вся работа сводится к ответам на три вопроса.
Первый. А удалось ли вам завершить чередование верхних и нижних пересечений нарисованной вами трассы? Не столкнулись ли при замыкании с двумя подряд идущими верхними или нижними пересечениями? Является ли полученный результат свойством именно вашей кривой линии? Можете ли вы нарисовать другую кривую линию с самопересечениями с другими свойствами при чередовании мостов?
(далее…)
Для любителей математики, просто, чтобы не забыть…
