Арбузный блог

В новой колонке на Информационном Буме. Приглашаю читать и решать.

Парадокс, но если выясняется, что человек интеллектуально развит, много читает, слушает классическую музыку, то многие будут к нему относиться не иначе, как к проклятому ботанику, умнику и ужасно скучному человеку.

Из дневника Zabriskie

Просто захотелось вспомнить красивые задачи, попадавшие в поле зрения. Знаю, что есть любители красивых задач, любители поковыряться с задачками и даже, самые утонченные, любители красивых условий геометрических задач. Задачи встречались в «Арбузном блоге», «Арбузном» и других форумах, в сообществах разных и на простых страничках бескрайней Сети. Спасибо всем авторам задач. Решения не привожу — прошу в комментарии в блоги, форумы, ЖЖ — адреса знаете. Рядом с истиной красотой все пояснения излишни, начинаем.

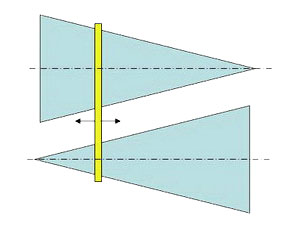
Концы нитки, продетой через кольцо, закреплены на концах А и В дощечки. Длина нити L больше расстояния АВ. Найти отрезки, на которые делится нитка свободно висящим кольцом при наклоне дощечки на угол ω от вертикали. Трением и весом нитки пренебречь.

Имеется в наличии: картина, веревка, два гвоздя, вбитых в стену. Нужно: повесить картину на стенку так, чтобы при вытаскивании любого из гвоздей она падала.

Кусок сыра имеет вид прямоугольного параллелепипеда 10×13×14. От него 10 раз отрезали полоски толщины 1 (каждая полоска была параллельна одной из граней параллелепипеда, но разные полоски могли быть параллельны разным граням). Какой наибольший объем может быть у оставшегося куска?
(далее…)

«Загадка строительства Великой пирамиды решена» – такие заголовки появляются в прессе раз в два-три года. И каждый раз «сенсация» постепенно меркнет, теряется на фоне неразрешённых вопросов, уходит в тень под давлением противоречий. Поэтому к ещё одной версии «трюка», применённого египтянами 4,5 тысячи лет назад, следует отнестись с осторожностью. Тем не менее последние открытия в Египте придали этой гипотезе новое дыхание.

Небольшое видео

{Скоростная чистка арбузов}

Кусок сыра имеет вид прямоугольного параллелепипеда 10x13x14. От него 10 раз отрезали полоски толщины 1 (каждая полоска была параллельна одной из граней па-раллелепипеда, но разные полоски могли быть параллельны разным граням). Какой наибольший объем может быть у оставшегося куска?

Это самая легкая из трёх задач, опубликованных сегодня Константином Кнопом.

Диана подняла задачу, многократно обуждаемую в разных сообществах: «Самолет разбегается на ленте транспортера, движущейся так, что компенсирует его скорость. Взлетит ли самолет?»

Теоретически ответ такой — если самолёт неподвижен относительно земли и окружающего его воздуха, то не взлетит, так как подъёмная сила возникает при обтекании крыльев воздухом. Известны модели, когда дополнительный поток воздуха на крылья создаётся пропеллерами — но хватит ли только этой составляющей для взлёта? Скорее всего нет.

Интересно, что в Википедии даже есть статья, посвященная этой задаче! Какие есть соображения — может, не все ещё учтено?

Прислал деда Митя. А вообще уже был пост с таким же заголовком :-)

Точнее, обновил версию движка до 2.6.3 — до этого была 2.3, поэтому и хакнули наверное :-)

В планах поменять тему, нравится Премиум как сейчас на Барбарисе…

приглядитесь — ползут по экрану

Про Арбузный блог написали на Дёрти.ру — это дало всплеск посещаемости :-)

Арбузы-чемпионы не кончились… просто скоро страшный праздник, а для него наряды делают из тыквы — подробнее здесь.

Порадовать друзей можно и отрезанными руками, скелетами и прочими вкусными вещами — об этом туточки

Подробности в статье «Как математика поможет в шнуровании ботинок«.

Интерактивная геометрическая разминка. Можно вместе с детьми…

С помощью простейших приспособлений можно на обычной циркулярной пиле получать разные профили.

Подробнее здесь. Спасибо ne0d1n’у — он дал ссылку на Cooler. Вопрос знатокам — какая кривая всегда в профиле?