Арбузный блог

Занятно — сайт не имеет никакого отношения к… но оформлен в арбузной теме. Ссылку прислал Дмитрий Малинин.

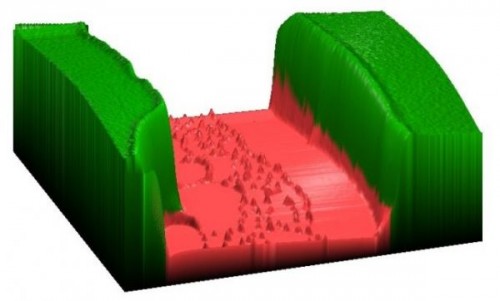
«Арбузная река». Ширина «русла» реки в 10 раз тоньше волоса человека — 8 мкм, высота «берегов» — 400 нм. Сканирование на АСМ. «Русло реки» — поверхность кремния, на которой видны остатки нанесённого полимера после его проявления и удаления, «берега реки» — полимер (PMMA). Источник.

Две картинки от художника Владимира Любарова. Направила Элеонора Шафранская. Напомню, что его троица стала юзерпиком у меня в ЖЖ.

sobol3v пишет в ru_olymp_math:
предлагаю еще 5 задач с американской олимпиады для студентов нематематических факультетов

1. Даны 4 идентичных апельсина, каждый радиусом 2 сантиметра. Из них составлена пирамида — три апельсина внизу, и один сверху посередине. Каждый апельсин касается трех других. Найти высоту пирамиды.

2. Пусть f(N) — сумма цифр составляющих N, пусть g(N) — произведение цифр, составляющих N. (пример: f(36)=9, g(36)=18)
Найти все положительные N, при которых 6*f(N)*g(N)=N^2

3. В группе был проведен экзамен (макс 100 баллов), но один студент не смог придти из-за болезни. Он пришел через неделю, чтобы таки его сдать. Перед экзаменом, он спросил преподавателя о результатах группы, на что получил ответ:
— Группа сдала не очень хорошо, и любой твой результат не изменит средний балл группы на более чем один балл (из 100).
Какова минимальная численность группы, где такой ответ будет возможным?

4. Два человека договорились встретиться. Каждый приедет в случайно выбранное время между 13.00 и 14.00 и прождет другого 15 минут перез отъездом. Каков шанс, что встреча таки состоится?

5. Шайба (размер, в целях задачи, считайте с одну точку) расположена в 1 метре от левой стороны и в пяти метрах от верхней и нижней сторон хоккейной коробки. Симметрично на другой стороне (1 метр от правой стороны и 5 метров от верхней и нижней сторон) расположена лунка, так же в целях задачи размером с одну точку (см диаграмму ниже). Размер коробки — 20 на 10 метров.

Хоккейст пытается ударить шайбу так, чтобы она отрикошетила от каждого бортика один (и только один) раз и попала в лунку. Найти угол между прямой, соединяющей исходную точку шайбы и лунки, и линией, по которой нужно будет нанести удар.
В целях задачи, сопротивление, трение и прочие физические параметры отсутствуют; угол отражения равен углу касания.

отсюда

Всех с праздником! это настоящий праздник — не религиозный и не политический… вот небольшая заметка о празднике на ПШ — прошу… А вот одна из попыток визуализации числа Пи…

ну и много всего в «Зоне Пи» на Арбузе…

просится на автару

Подарок от se_re_ne

Этот банер крутится в ротации на юФоруме.. :-) Ну вы поняли — к чему это… С праздником, девочки!

Оказалось 03.03.09 все математики на Западе, которые знают что это такое, отмечают День квадратного корня. Отсюда. Спасибо!

Стало быть следующий праздник через 7 лет, один месяц и 1 день… А кто перечислит все такие праздники?

Сталкивающиеся галактики Arp 274. Фото с сайта hubblesite.org

NASA завершило интернет-голосование по выбору следующей цели для орбитального телескопа «Хаббл», сообщается на сайте проекта. Победителем стали сталкивающиеся галактики Arp 274. В период со 2 по 5 марта «Хаббл» сделает полноцветную фотографию этого объекта в высоком разрешении. Она будет опубликована на сайте проекта «100 часов астрономии».

(далее…)

Американский математик Эндрю Хикс разработал сложные компьютерные модели, с помощью которых он может изготавливать зеркала изощрённой формы с необычными свойствами. На компьютере просчитывается, как будет отражаться свет с десятков тысяч граней — и в результате можно сделать, например, зеркало, в котором текст читается нормально или 360-градусная панорама отображается без искажений на плоской поверхности.
(далее…)

Пишут, что эту и похожие задачки MS использует на своих собеседованиях:
Злобный демон поймал много гномов (их точное количество неизвестно). После этого во время «инструктажа при приеме на работу» в свою компанию демон прикрепил каждому из гномов на лоб красный или зеленый драгоценный камень. Демон сообщает каждому своему новому рабу гному, что теперь у того на лбу драгоценный камень, который невозможно удалить. Ни сам демон, ни другой гном не скажут, какого цвета этот камень (гномам строго запрещено разговаривать).
Каждое утро гномы строятся. Это делается для того, чтобы демон мог их пересчитать и убедиться, что ни один из гномов не убежал.
В один прекрасный день демону гномы надоели, и он решил от них избавиться. Он объявляет гномам, что отпустит их всех на свободу, если они сумеют правильно определить, какого цвета прикрепленный у каждого из них на лбу камень. Он дает им одну подсказку: есть по крайней мере один гном с зеленым камнем и один — с красным. Чтобы обрести свободу, гномы во время утреннего построения должны (им по прежнему нельзя разговаривать) подать демону правильный сигнал: все гномы с красным камнем во лбу должны выйти из строя на один шаг, а все те, у кого зеленый камень, — остаться в строю. Если они при этом не допустят ни одной ошибки — все гномы смогут отправиться домой и снова работать на своих любимых угольных шахтах. Если же они допустят ошибку — все будут казнены прямо на месте.
Время, которое дается гномам для определения цвета камней, не ограничено. Они все обладают безупречной логикой и очень хотят вернуться домой. Как им нужно поступить?
Повторюсь: гномы НИКАК не могут общаться. У них есть неограниченное число построений для решения вопроса и только одна попытка.
PS: Гномы в данной задаче — безупречно логичные существа, у них абсолютное зрение, память, понимание логики других гномов.

Взято отсюда — там и комменты есть…