Рисуем картинки с помощью кривой Гильберта

Воскресенье, 12 Февраль, 2012 | Рубрика: Матем. картинки

В субботу на прошлой неделе «дело было вечером, делать было нечего», и мы с хабраюзером sourcerer разговаривали не понятно о чём. И почему-то речь зашла речь о задаче обратной к задаче построения графика функции по её выражению. То есть, например, у нас есть выражение y(x) = (cos0,5x ⋅ cos 200x + |x|0,5 − 0,7)(4 − x2)0,01. График такой функции чем-то напоминает сердечко. Но нам был интересен обратный вопрос, как, имея, например, изображение сердечка, получить выражение для функции, графиком которой будет это самое сердечко.

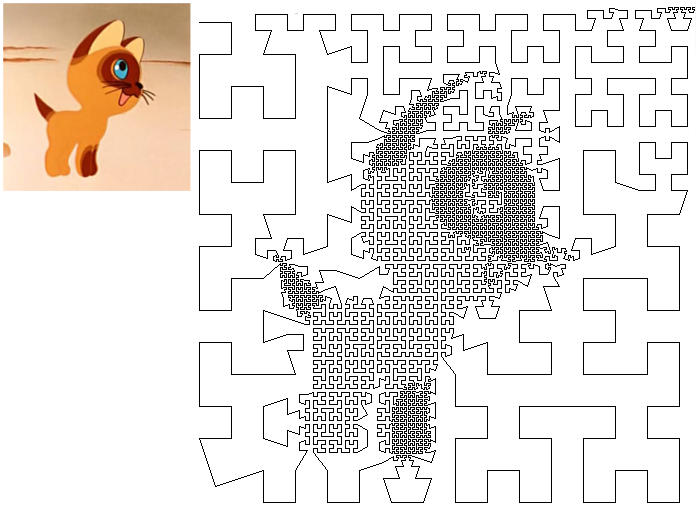
Какие-нибудь ряды Фурье вспоминать не хотелось, а хотелось чего-то простого и красивого. Мы начали вспоминать известные нам результаты, связанные с этим вопросом. В результате получилась программка, которая по изображению генерирует ломаную линию, чем-то напоминающую исходное изображение. На примере котёнка по имени Гав это выглядит примерно так (смотреть лучше издалека):

Если интересно как такое сделать, а также узнать про формулу конопли, формулу, график которой является этой же формулой, то добро пожаловать под хабракат. (Будет много картинок.)

Итак, вспомним некоторые результаты.

Формула конопли. Примерно в 2005 году активно разрабатывалась и обсуждалась формула конопли. Простые формулы в полярных координатах вида

  1. R(t) = (1 + sin t)(1 + 0,9 ⋅ cos 8t)(1 + 0,1 ⋅ cos 24t),
  2. R(t) = (1 + sin t)(1 − 0,9 ⋅ |sin 4t|) ⋅ (0,9 + 0,05 ⋅ cos 200t),
  3. R(t) = (1 + sin t)(1 + 0,9 ⋅ cos 8t)(1 + 0,1 ⋅ cos 24t) (0,5+0,05 ⋅ cos 140t)

конечно обладают симпатичными графиками, но всё это ничто по сравнению с результатом Антона Сухинова.

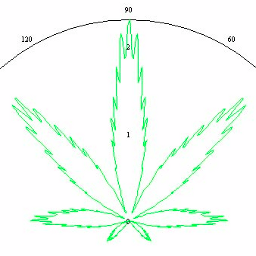
Что же сделал Антон Сухинов? Он в 2005 на арбузном форуме предложил следующую замысловатую формулу (если я нигде не ошибся при наборе):

Тогда, рисуя только те точки для которых F(a, r) > 0 и выбирая цвет в зависимости от значения функции, получаем следующее изображение:

С ума спрыгнуть, не правда ли?

Формула Таппера. Рассмотрим неравенство
, и пусть число k равно
48584506361897134235820959624942020445814005879832445494830930850619347
04708809928450644769865524364849997247024915119110411605739177407856919
75432657185544205721044573588368182982375413963433822519945219165128434
83329051311931999535024137587652392648746133949068701305622958132194811
13685339535565290850023875092856892694555974281546386510730049106723058
93358605254409666435126534936364395712556569593681518433485760526694016
12512669514215505395545191537854575257565907405401579290017659679654800
64427829131488548259914721248506352686630476300.

Оказывается множество точек (x, y − k) удовлетворяющих этому неравенству и таких, что 0 ≤ x ≤ 106 и k ≤ y ≤ k + 17, выглядит следующим образом:

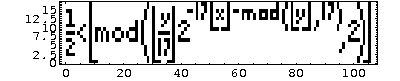
А это снова само неравенство. Понятно, конечно, что просто-напросто в числе k зашифровано изображение, но тем не менее результат очень красивый и не понятно как такое вообще можно было придумать.
Более подробно можно почитать в википедии: Tupper’s self-referential formula, а мы перейдём от частных результатов к массовым методам.

Системы итерируемых функций. Наверное, каждый, кто хоть немножко сталкивался с фракталами, знает, что такое системы итерируемых функций. СИФ позволяет с помощью пары десятков чисел получать картинки очень похожие на реальные листья, деревья, ветки:

Идея о том, что можно попытаться решить обратную задачу — по заданному изображению получить набор чисел, описывающих СИФ, позволила Майклу Барнсли придумать фрактальное сжатие. Какая-то попытка рассказать о фрактальном сжатии уже предпринималась на хабре: Основы фрактального сжатия изображений. Но тем, кто хочет разобраться детально порекомендую первую половину книги «Фракталы и вейвлеты для сжатия изображений в действии» С. Уэлстида.

Фрактальные строки. На самом деле в алгоритме фрактального сжатия используются не системы итерируемых функций, а так называемые системы частичных итерируемых функций. Тем не менее есть класс изображений, для которых легко придумать именно СИФ, аттракторами которых они являются. Такими изображениями являются фрактальные строки. Фрактальная строка — это слово, каждая буква которого состоит из уменьшенных копий данного слова и так далее. На примере слова «ХАБР» это выглядит как-то так:

Несложно понять как такое сделать для произвольного слова, достаточно потратить немного времени, чтобы представить каждое слово в виде набора параллелограммов. Как минимум лет пять назад это было сделано. Подробное описание и код можно найти в статье Фрактальные строки.

Портрет В.-Й. Мёллера. Листая книгу «Фракталы, хаос, степенные законы. Миниатюры из бесконечного рая» М. Шредера, можно наткнуться на следующую иллюстрацию:

Выглядит это очень симпатично, и понятно, что такое можно сделать с произвольным изображением. О том, как это было нарисовано, в книге не рассказывается, но не сложно догадаться самому.

Для начала нужно взять алгоритм построения кривой Гильберта. Но не с помощью каких-нибудь L-систем, а честный рекурсивный алгоритм. А дальше модифицируем его следующим образом. Если яркость квадратика больше заданного порога и в четырёх его подквадратиках кривую рисовать не нужно, то считаем, что и в самом квадратике рисовать кривую не нужно. Хотя наверное проще понять из кода, приведённого ниже.

Point2D[] drawHilbertCurve(Point2D p, double size, int d) { Point2D q = new Point2D.Double( p.getX() + size * sqrt(2) * cos(PI * (d + 0.5) / 2), p.getY() + size * sqrt(2) * sin(PI * (d + 0.5) / 2)); if (size <= 2) { if (blockIsWhite(p, q)) { return null; } else { Point2D cc = new Point2D.Double( p.getX() + size * sqrt(2) * cos(PI * (d + 0.5) / 2) / 2, p.getY() + size * sqrt(2) * sin(PI * (d + 0.5) / 2) / 2); return new Point2D[]{cc, cc}; } } else { Point2D cl = new Point2D.Double( p.getX() + size * cos(PI * (d + 1) / 2) / 2, p.getY() + size * sin(PI * (d + 1) / 2) / 2); Point2D cc = new Point2D.Double( p.getX() + size * sqrt(2) * cos(PI * (d + 0.5) / 2) / 2, p.getY() + size * sqrt(2) * sin(PI * (d + 0.5) / 2) / 2); Point2D br = new Point2D.Double( p.getX() + size * cos(PI * d / 2), p.getY() + size * sin(PI * d / 2)); Point2D[] p1 = drawHilbertCurve(cl, size / 2, d - 1); Point2D[] p2 = drawHilbertCurve(cl, size / 2, d); Point2D[] p3 = drawHilbertCurve(cc, size / 2, d); Point2D[] p4 = drawHilbertCurve(br, size / 2, d + 1); if (p1 == null && p2 == null && p3 == null && p4 == null && blockIsWhite(p, q)) { return null; } else { if (p1 == null) { p1 = new Point2D[2]; p1[0] = p1[1] = new Point2D.Double( cl.getX() + size * sqrt(2) * cos(PI * (d - 0.5) / 2) / 4, cl.getY() + size * sqrt(2) * sin(PI * (d - 0.5) / 2) / 4); } if (p2 == null) { p2 = new Point2D[2]; p2[0] = p2[1] = new Point2D.Double( cl.getX() + size * sqrt(2) * cos(PI * (d + 0.5) / 2) / 4, cl.getY() + size * sqrt(2) * sin(PI * (d + 0.5) / 2) / 4); } if (p3 == null) { p3 = new Point2D[2]; p3[0] = p3[1] = new Point2D.Double( cc.getX() + size * sqrt(2) * cos(PI * (d + 0.5) / 2) / 4, cc.getY() + size * sqrt(2) * sin(PI * (d + 0.5) / 2) / 4); } if (p4 == null) { p4 = new Point2D[2]; p4[0] = p4[1] = new Point2D.Double( br.getX() + size * sqrt(2) * cos(PI * (d + 1.5) / 2) / 4, br.getY() + size * sqrt(2) * sin(PI * (d + 1.5) / 2) / 4); } drawLine(p1[0], p2[0]); drawLine(p2[1], p3[0]); drawLine(p3[1], p4[1]); } return new Point2D[]{p1[1], p4[0]}; } }

 

 

boolean blockIsWhite(Point2D p, Point2D q) { int l = (int) min(p.getX(), q.getX()); int r = (int) max(p.getX(), q.getX()); int t = (int) min(p.getY(), q.getY()); int b = (int) max(p.getY(), q.getY()); double c = 0; for (int i = l; i < r; ++i) { for (int j = t; j < b; ++j) { c += (srcImage.getRGB(i, j) & 0x0000FF) / 255.0; } } return c / ((b - t) * (r - l)) > threshold * (1 - log(2) / log(b - t)); }

Перед тем, как изображение скармливалось программке, оно переводилось в оттенки серого и опытным путём подстраивалась яркость и контрастность. Например, вот что получилось, когда программку натравили на тукса:

Исходный код программки.

Если кто-то знает ещё какие-то красивые результаты из обсуждаемой области, то напишите об этом, пожалуйста, в комментариях.

 

Источник Хабр.